Video: Introduction to Quantum Electrodynamics
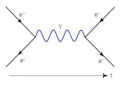
Development of QED started in the 1920s. It is a field theory that describes the electromagnetic interactions between charged fundamental particles, for example electrons and positrons, via photons. From the late 1920s, Paul Dirac and Wolfgang Pauli, and others, started to apply quantum mechanics to fields resulting in quantum field theory. QED as we know it today was first suggested in the 1940s. The development of QED was the first use of the renormalization mathematical technique, as well as the first use of Richard Feynman's diagrammatical technique now called Feynman Diagrams; see a simple example below. Calculating the magnitude of the particle/field interactions uses perturbation theory. There is an excellent video from Fermilab explaining this technique.
Feynman diagrams represent this pictorially. While QED does not predict exactly what would happen in a particular experiment, it gives the probability of what would happen. The results of these probabilities agree with experiment to a remarkable degree of accuracy; for example, experiments based on the electromagnetic fine structure constant, have shown QED to be accurate to better than 10 parts in one billion. Measurement of the anomalous magnetic dipole moment of the electron have yielded accuracy to approximately 1 part in a billion. Because of the extreme accuracy of its predictions, QED is sometimes called the "Jewel of Physics".
Feynman diagrams represent this pictorially. While QED does not predict exactly what would happen in a particular experiment, it gives the probability of what would happen. The results of these probabilities agree with experiment to a remarkable degree of accuracy; for example, experiments based on the electromagnetic fine structure constant, have shown QED to be accurate to better than 10 parts in one billion. Measurement of the anomalous magnetic dipole moment of the electron have yielded accuracy to approximately 1 part in a billion. Because of the extreme accuracy of its predictions, QED is sometimes called the "Jewel of Physics".
Physics
-
Quantum Physics
Quantum Electrodynamics
Feynman Diagram
In 1965, Richard Feynman, Julian Schwinger and Sin-itero Tomonaga, received the Nobel prize for their work in quantum electrodynamics. A Nobel Prize can be shared by a maximum of three people, so, controversially, Freeman Dyson was omitted, though his contribution was substantial.
Here is a brief description of QED. The video above gives a description starting from the basics of the behavior of light.
Here is a brief description of QED. The video above gives a description starting from the basics of the behavior of light.
Menu: